https://www.acmicpc.net/problem/17387
17387번: 선분 교차 2
첫째 줄에 L1의 양 끝 점 x1, y1, x2, y2가, 둘째 줄에 L2의 양 끝 점 x3, y3, x4, y4가 주어진다.
www.acmicpc.net
직선의 방정식과 선분의 양 끝 좌표를 이용해 풀어보려고 했지만... 실패했다. 아이디어 자체는 실현 가능한 거 같아서 나중에 도전해볼 예정
0.
설명하기에 앞서 일단 나는 벡터를 잘 모른다. 선형대수학 나름 열심히 배웠는데.... 어쨌든 그래서 이 문제의 정석? 풀이에 사용된 CCW 알고리즘의 식을 해설할 능력은 없다. 다만 이 문제에서 식을 응용할 필요는 없고 결과의 의미만 이해할 수 있으면 된다. 시각적으로 접근하면 금방 이해할 수 있다.
1.
CCW는 counter clockwise, 즉 반시계방향을 뜻한다. CCW 함수는 점 A, B, C의 x, y 좌표 3개씩을 인수로 받아 세 점이 순서대로 반시계방향을 이루는 지 판별한다. 식은 다음과 같으며, 뒤에 다시 설명하겠지만 연산한 값 대신 양수, 0, 음수 판별 결과만 반환하면 된다. 그리고 그렇게 안 하면 틀린다.
int ccw(pos a, pos b, pos c) {
ll temp = (a.x * b.y + b.x * c.y + c.x * a.y) - (a.y * b.x + b.y * c.x + c.y * a.x);
if (temp > 0)
return 1;
if (temp == 0)
return 0;
else
return -1;
}
왜 그런지는 벡터 외적 연산을 알고 있다면 검색해서 쉽게 이해할 수 있다... 이해할 수 있어서 부럽다... 하지만 나처럼 기하와 벡터 과목을 제대로 안 배워 벡터 연산이 익숙하지 않은 사람은 이렇게만 이해하면 된다.

" 대충 무슨 식이 있는데, 그 식을 복붙해와서 세 점을 넣었을 때 (순서에 유의할 것)
값이 양수이면 반시계 방향, 음수이면 시계 방향, 0이면 일직선 상으로 세 점이 위치한 것이다 "
이제 CCW의 인수에 한 선분의 양 끝점과 다른 한 점을 순서대로 넣음으로써 선분에 대한 점의 방향성을 확인할 수 있다.
2.
한 점의 방향만 확인하면 뭔가 부족하다. 이렇게 생각해보자.
선분 AB가 있다. 두 점 C, D를 찍어 AB와 교차하는 선분 CD를 만들고자 한다. 그럼 우리는 상식적으로 이렇게 점을 찍을 것이다.

다음 그림을 보자. 자기 멋대로 이렇게 점을 찍는 개구쟁이들은 선분을 교차시킬 수 없다.

그런데 여기서, CCW 함수로 선분 AB와 C, D의 방향성을 따져보면 어떨까?

선분 AB와 점 C, D가 이루는 방향은 같다. CCW 결과를 이용해 나타내자면 CCW(A, B, C) * CCW(A, B, D) > 0이다. 참고로 직접 해보면 알겠지만 A와 B의 순서를 바꿔도 결과는 같다. 어쨌든, 두 CCW 값의 곱이 양수이면 점이 같은 방향에 있다는 뜻이므로 선분을 교차시킬 수 없다.
하지만 이 경우는 어떨까?

분명 방향이 반대, 그러니까 두 CCW 값의 곱이 -1이긴 한데... 선분 AB와 CD는 교차하지 않는다. 이는 한 쪽 선분에서만 확인했기 때문이다. 같은 위치에서 AB를 점, CD를 선분으로 만들어보자.

어라, 이번엔 두 점이 같은 방향에 위치한다.
일단 이번에 입수한 정보는 다음과 같다. 선분 AB에서 점 C, D에 대해 CCW를 수행해 곱한 값이 res1, 선분 CD에서 점 A,B에 수행해 곱한 값이 res2라고 하자. res1과 res2 중 어느 하나라도 양수일 경우 위의 그림들 중 하나에 해당하므로 선분은 교차되지 않는다.
int answer;
if(res1 > 0 || res2 > 0)
answer = 0;
3.
res1과 res2가 둘 다 양수가 아닐 경우를 살펴보자.
먼저 둘 다 음수일 경우, 한 선분의 두 끝점이 다른 선분에 대해 서로 반대 방향에 위치해야 하므로, 어떤 경우에서도 선분이 교차한다.
하나가 0인 경우는 어떨까? 그러니까 하나만 0인 경우. 이 경우에는 다른 하나의 값을 확인해보면 된다.
점 C가 선분 AB와 같은 직선 상에 있다고 할 때, C는 선분 AB 내부 또는 외부에 위치할 수 있다.
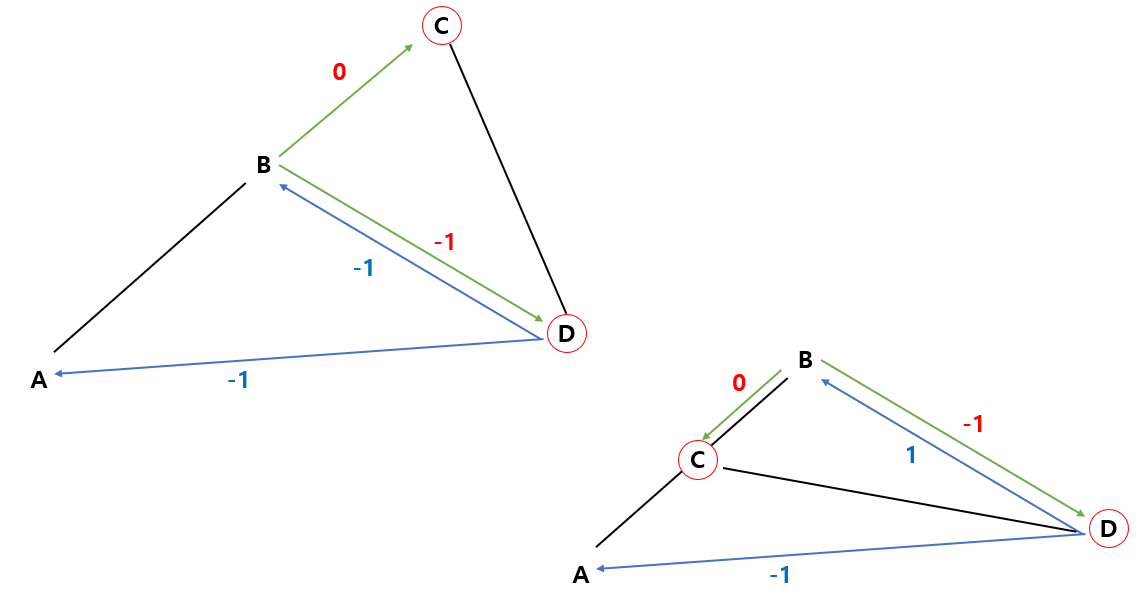
파란색 선에 주목하자. C가 선분 외부에 위치할 경우, 첫 번째 그림처럼 선분 CD에서 점 A, B에 대해 CCW를 구해보면 그 곱이 양수가 나온다. 반면 C가 선분 내부에 있을 경우, 두 번째 그림처럼 선분 CD에 대해 A와 B는 다른 방향에 존재할 수밖에 없으며, CCW의 곱은 음수가 될 것이다.
즉 res1의 값이 0이면, 일직선 상의 점이 선분 내부에 존재할 경우 res2가 -1, 외부에 존재할 경우 res2가 1이다. 따라서 이 경우는 식을 새로 작성할 필요 없이 위의 조건문에서 걸러진다. 개꿀
그럼 둘 다 0인 경우는?
선분 A, B에 대해 C도 같은 직선 상에, D도 같은 직선 상에 위치한다는 말은 결국 선분 CD 전체가 선분 AB와 동일 선상에 놓여있다는 말과 같다. 그럼 이번엔 머리 아픈 벡터 연산 대신, 좌표만 확인하면 된다.
선분 AB의 동일 선상에 점 C, D를 찍으려 한다. 다음 두 경우를 보자.
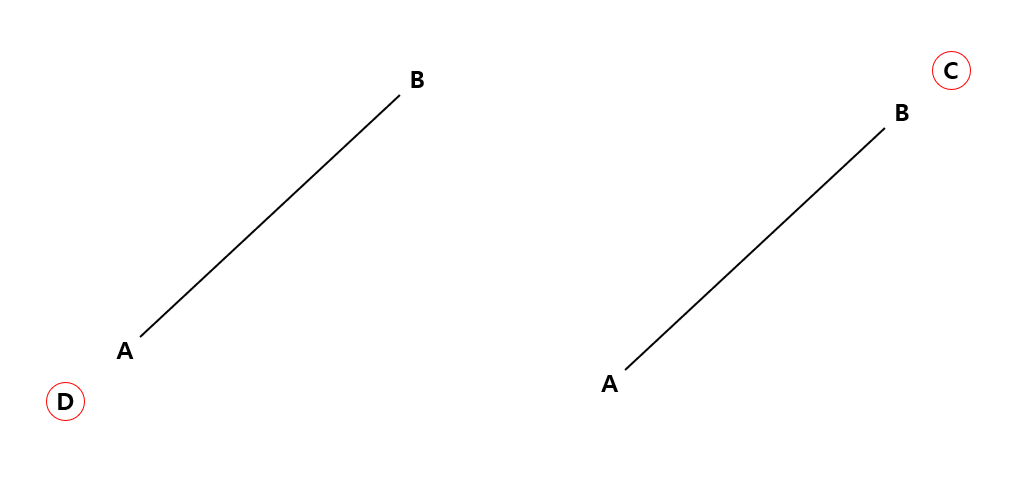
선분 CD에서 점 C는 반드시 점 D보다 왼쪽 아래 방향에 위치한다고 가정하자. 위의 두 경우에서 점 C와 점 D를 저렇게 엉망으로 찍어버리면 나머지 한 점을 어디에 찍던간에 두 선분이 교차할 수 없다.
즉, P1 < P2를 '점 P1이 점 P2보다 왼쪽 아래에 위치한다' 라고 정의하면, 동일 선상의 두 선분이 교차하기 위해서는 D < A이거나 B < C이면 안 된다.
소스 코드
분기 조건은 저걸로 끝이다. 이제 잘 구현만 하면 되는데, 주의할 점이 몇 가지 있다.
1) CCW 오버플로우
CCW에서 0, 1, -1 대신 계산 결과 자체를 반환할 경우, CCW 식이 (a.x * b.y + b.x * c.y + c.x * a.y) - (a.y * b.x + b.y * c.x + c.y * a.x)이므로, 대충 최대 N^2의 값을 반환한다고 볼 수 있다. 한 선분에 대한 두 점의 방향성을 계산하기 위해 우리는 두 CCW 값을 곱해야 하므로, 나올 수 있는 최댓값은 N^2 * N^2 = N^4이다. 입력 N의 최댓값이 1000000, 2^20이기 때문에 N^4 = 2^80으로 아무리 long long 자료형을 사용해도 오버플로우가 발생할 수 있다. 그러니 고집은 거두고 순순히 판별 결과만 반환하자.
2) 둘 다 0인 경우
이 부분은 저마다 다양한 풀이를 보여준 거 같은데, C++로 문제를 푼다면 내 체감상 pair를 사용하는 게 제일 편하다.
pair 클래스 자체가 우리에게 필요한 '<' 연산자 오버로드를 지원하기 때문이다. 그리고 위에 언급한대로 점 A, C가 점 B, D보다 왼쪽 아래에 존재한다는 가정을 실현하기 위해 swap 함수를 사용하자. 여기서도 pair 클래스 인자를 잘 받아준다. A > B, C > D일 경우 서로를 바꿔주면 된다.
코드
int ccw(pos a, pos b, pos c) {
ll temp = (a.x * b.y + b.x * c.y + c.x * a.y) - (a.y * b.x + b.y * c.x + c.y * a.x);
if (temp > 0)
return 1;
if (temp == 0)
return 0;
else
return -1;
}
int main() {
FASTIO;
ll x1, x2, x3, x4;
ll y1, y2, y3, y4;
cin >> x1 >> y1 >> x2 >> y2;
cin >> x3 >> y3 >> x4 >> y4;
int ccw1 = ccw({ x1, y1 }, { x2,y2 }, { x3,y3 }) * ccw({ x1,y1 }, { x2,y2 }, { x4,y4 });
int ccw2 = ccw({ x3, y3 }, { x4,y4 }, { x1,y1 }) * ccw({ x3,y3 }, { x4,y4 }, { x2,y2 });
int res = 1;
//둘 다 음수일 경우만
if (ccw1 <= 0 && ccw2 <= 0) {
//두 선분이 일직선
if (ccw1 == 0 && ccw2 == 0) {
//pair 클래스 활용
pair<int, int> p1 = { x1, y1 };
pair<int, int> p2 = { x2, y2 };
pair<int, int> p3 = { x3, y3 };
pair<int, int> p4 = { x4, y4 };
//왼쪽 아래 정렬
if (p1 > p2)
swap(p1, p2);
if (p3 > p4)
swap(p3, p4);
//구간 겹치는지 확인
if (p4 < p1 || p2 < p3)
res = 0;
}
}
//하나라도 양수이면 교차하지 않음
else
res = 0;
cout << res << endl;
}
'백준' 카테고리의 다른 글
| 백준 3015 - 오아시스 재결합 (0) | 2023.10.03 |
|---|---|
| 백준 1208 - 부분수열의 합 2 (0) | 2023.09.13 |
| 백준 9466 - 텀 프로젝트 (1) | 2023.09.12 |
| 백준 2623 - 음악프로그램 (0) | 2023.09.07 |
| 백준 1202 - 보석 도둑 (2가지 풀이) (0) | 2023.09.06 |