백준 BaaaaaaaaaaarkingDog님이 제작하신 문제집을 사용합니다
링크 : https://www.acmicpc.net/workbook/view/7314
문제집: 0x0B강 - 재귀 (BaaaaaaaaaaarkingDog)
www.acmicpc.net
모든 문제를 풀고 필요할 경우 코멘트를 작성한다.
여기서 말하는 재귀는 '분할 정복' 알고리즘을 포함한다.
재귀와 분할 정복은 어떻게 분할할 지, 재귀의 끝(base case)에서 무엇을 하는지 2가지만 신경써주면 된다.
이 두 가지만 논리적으로 설정하면 속는 셈 치고 실행해보자. 답이 잘 나온다.
1629번 : 곱셈 → 사실 이 문제는 주로 반복문으로 구현한다. 구현보다 논리 자체를 알아두자.
'분할 정복을 이용한 거듭제곱'에 대해 자세히 설명해주는 사이트를 찾아보자. 여기 말고...
자주 하는 실수
이런 류 문제를 풀 때는 오버플로우에 주의해야 한다. 연산 과정에서 생성될 수 있는 최댓값을 생각해보자.
이 문제에서는 아무리 나머지 연산을 해줘도 (2^31 - 1) * (2^31 - 1)이라는 중간 결과가 생길 수 있다.
따라서 안전하게 long long 자료형을 사용해줘야 한다. 사실 그냥 long long은 남발할 수록 안전해진다.
11729번 : 하노이 탑 이동 순서 → 탑 전체를 옮기는 과정을 3개의 작은 과정으로 쪼개보자.
5층 탑을 1번에서 3번 장대로 옮긴다. 어떻게 해야 할까? 전체 과정을 간소화하면 이렇다.
4층 (1번부터 4번) 탑을 1번에서 2번 장대로 옮긴다. 5번 원판을 3번 장대로 옮긴다. 4층 탑을 2번에서 3번 장대로 옮긴다.
5층, 1->3이라는 동작은 (4층, 1->2)와 (원판 5, 1->3)과 (4층, 2->3)이라는 3개의 동작으로 나눠진다.
이제 4층 탑을 1번에서 2번 장대로 옮기려면 어떻게 할까?
3층 탑을 1번에서 3번 장대로 옮긴다. 4번 원판을 2번 장대로 옮긴다. 3층 탑을 3번에서 2번 장대로 옮긴다.
일반화하면 다음과 같다.
N층 탑을 A번에서 B번 장대로 옮기기
- N-1층 탑을 A번에서 C(A, B 말고 나머지 장대)번 장대로 옮긴다.
- N번 원판을 B번 장대로 옮긴다.
- N-1층 탑을 C번에서 B번 장대로 옮긴다.
base case : N이 1일 때, C를 거칠 필요 없이 그냥 옮기면 된다.
1074번 : Z → N이 3일 때의 예시에서, 4분할한 정사각형의 왼쪽 맨 위 숫자는 모두 16의 배수임을 발견할 수 있다.
다시 말하면 4분할한 정사각형 각각에 대해, 같은 위치의 숫자는 모두 16의 배수만큼 차이가 난다. 이 정보를 활용해보자.
r행 c열의 칸이 현재 크기 64의 정사각형을 4분할 했을 때 어디에 위치하는 지 확인한다.
왼쪽 위일 경우, 크기 16의 정사각형에서 다시 탐색한다.
오른쪽 위일 경우, 왼쪽 위에 있을 때와 동일한 방식으로 탐색한 뒤 그 결과에 16을 더해주면 된다.
왼쪽 아래일 경우 32, 오른쪽 아래일 경우 48을 더해주면 된다.
base case : 크기가 4인 정사각형에서는 2차원 배열 arr[2][2] = {0,1,2,3} 순서로 번호가 부여된다.
17478번 : 재귀함수가 뭔가요? → 어질어질한 출력 예시의 구조만 잘 파악하면 간단해진다.
코드 간결화를 위해 문자열이나 길이 4의 밑줄을 미리미리 변수로 저장하자. 잘못 복붙하면 띄어쓰기가 깨지는 경우가 있으니 주의. 그리고 큰 따옴표나 줄 바꿈 처리도 주의.
1780번 : 종이의 개수 → 개수를 기록할 count[3] 배열을 사용하면 편하다.
현재 종이의 왼쪽 맨 위를 기준점으로 잡고 종이의 모든 값을 기준점과 비교한다. 모두 같으면 배열에서 기준점에 해당하는 원소를 증가시킨다. 값의 범위가 -1~1이므로 배열 인덱스에 맞게 1을 더해 count[값+1]++;
하나라도 다르다면 종이를 9개로 쪼개 각 위치에서 다시 기준점을 설정하고 비교, 즉 재귀함수를 호출한다. 아래와 같이 이중 반복문으로 구현하면 깔끔하다.
int subSize = size / 3;
for (int i = 0; i < 3; i++)
for (int j = 0; j < 3; j++)
recursion(arr, sr + i * subSize, sc + j * subSize, subSize);
base case : 길이가 1일 경우 즉시 count[기준점 값 + 1]++;
아래 두 문제는 이 문제와 비슷하게 풀 수 있다.
2630번 : 색종이 만들기 → 위 문제에서 숫자만 바꿔주면 된다
1992번 : 쿼드트리 → 재귀 호출 전 괄호를 열고, 복귀하면 괄호를 닫는다. base case에서는 괄호를 열지 않는다.
2447번 : 별 찍기 - 10 → 함수 내에서 직접 출력하면 줄바꿈을 처리하기 어렵다. 어려운 건지 불가능한 건지
출력 내용을 저장할 문자열 배열을 사용하자.
문자열을 공백문자로 채워놓고 별이 채워지는 부분만 계산하면 된다. 11번 문제를 풀고 나서야 깨달았다.
문자열 배열 선언을 이런 식으로 해보자.
//string(int count, char c) : 문자열을 c 문자로 count 길이만큼 초기화
vector<string> arr(N, string(N, ' '));
2448번 : 별 찍기 - 11 → 너무 헤맸다... 문자열을 공백문자로 채워놓고 별이 채워지는 부분만 계산하면 된다.
* 이번에는 base case가 1이 아니다.
14956번 : Philosopher's Walk → Z 문제를 변형했다. 그런데 좀 많이 많이 어렵게.
조잡한 설명은 아래에
0.
원래의 정사각형을 4개의 작은 정사각형으로 나누고, 남은 거리에 따라 4개 중 하나를 골라 다시 탐색하면 된다.
그런데 어떻게 골라야 할까? 선택을 위해 현재 '도형의 각도'와 '방문 순서'를 고려해야 한다.
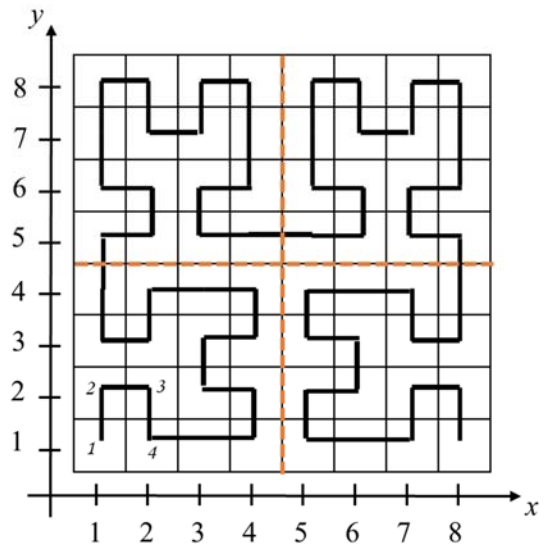
1.
예제 입력 2를 이용해 더 자세히 알아보자. 주황색 십자를 기준으로 나눠진 4개의 정사각형이 좌표평면의 4사분면을 나타낸다고 하자. 그러면 m = 19일 때 몇 사분면을 다음 탐색 위치로 선택해야 할까?
왼쪽 맨 아래부터 도형을 따라 이동할 경우, 4개의 사분면을 3사분면 - 2사분면 - 1사분면 - 4사분면 순서대로 방문하게 된다. 그리고 m 이 19인 지점은 두 번째(m / 16 + 1) 로 방문하는 사분면 안에 있다. 따라서 재귀 호출을 이용해 길이를 반으로 줄이고 2사분면으로 이동해 탐색을 계속하면 된다.
2.
그런데 이 도형이 오른쪽으로 90도 돌아가있으면, 그래도 3-2-1-4 순서로 방문하게 될까?

아니다. 다시 왼쪽 아래부터 이동해보면 방문 순서는 3-4-1-2가 된다.
이 도형에서 두 번째로 방문하는 사분면은 4사분면이다. 즉 우리는 m을 작은 정사각형의 크기로 나눠 '방문 순서'를 구할 수 있으며, 방문 순서와 도형의 각도(회전 상태)를 이용해 다음에 탐색할 사분면을 선택할 수 있다. 이를 4x4 배열로 정의해둬도 좋다.
사분면만 선택했다고 끝이 아니다. 재귀함수의 인자가 될 작은 정사각형 안 도형의 각도도 다시 구해야 한다. 예를 들어 위 그림에서 두 번째로 방문하는 사분면을 선택했다면, 작은 도형은 아래 그림처럼 여전히 오른쪽으로 90도 돌아간 상태임을 확인할 수 있다. 작아진 도형의 각도 역시 4x4 배열을 이용해 결정해야 한다.

설명 능력이 부족해 코드를 첨부했으니... 질문이 있으면 댓글 바랍니다
#define _CRT_SECURE_NO_WARNINGS
#include <bits/stdc++.h>
using namespace std;
int nxtQuad[4][4] = { {3,2,1,4},{3,4,1,2},{1,4,3,2},{1,2,3,4} };
int nxtDeg[4][4] = { {1,0,0,3},{0,1,1,2},{3,2,2,1},{2,3,3,0} };
void recursion(int sr, int sc, int size, int dist, int deg) {
if (size == 2) {
switch (nxtQuad[deg][dist]) {
case 1:
cout << sc + 1 << ' ' << sr + 1;
break;
case 2:
cout << sc << ' ' << sr + 1;
break;
case 3:
cout << sc << ' ' << sr;
break;
case 4:
cout << sc + 1 << ' ' << sr;
break;
}
cout << endl;
return;
}
size /= 2;
int sqr = size * size;
int seq = dist / sqr;
dist -= seq * sqr;
switch (nxtQuad[deg][seq]) {
case 1:
recursion(sr + size, sc + size, size, dist, nxtDeg[deg][seq]);
break;
case 2:
recursion(sr + size, sc, size, dist, nxtDeg[deg][seq]);
break;
case 3:
recursion(sr, sc, size, dist, nxtDeg[deg][seq]);
break;
case 4:
recursion(sr, sc + size, size, dist, nxtDeg[deg][seq]);
}
}
int main() {
int n, m;
cin >> n >> m;
recursion(1, 1, n, m - 1, 0);
}푼 문제 : 10/10
총 소요 시간 : 4시간 20분
배운 스킬!!!!
답만 계산하기 : BFS 거리 계산처럼, 전체를 완성한 뒤 답에 해당하는 부분을 선택하는 문제 유형이 있다. 반면 전체는 쌩까고 답만 찾으면 되는 유형도 있다.
Z나 Philosopher's Walk 문제에서는 배열에 일일히 값을 채워넣을 필요 없이, '확인할 필요 없는 부분'을 잘라나가면서 목표 지점에 도달하기만 하면 된다. 별 찍기 문제에서는 초기화만 잘 해놓으면 공백문자 출력은 신경 쓸 필요가 없다.
문제의 난이도가 올라갈 수록 생각해야 할 요소는 많아진다. 답을 얻기 위해 꼭 필요한 계산이 무엇인지 따져보고 필수가 아닌 부분은 과감하게 잘라내자.
'백준 > 문제집(유기)' 카테고리의 다른 글
| 백준 문제집 풀이 10 - 백트래킹 (0) | 2023.11.08 |
|---|---|
| 백준 문제집 풀이 8 - BFS (0) | 2023.10.06 |
| 백준 문제집 풀이 7 - 스택의 활용 (1) | 2023.10.06 |
| 백준 문제집 풀이 6 - 덱 (1) | 2023.10.06 |
| 백준 문제집 풀이 5 - 큐 (1) | 2023.10.06 |