백준 2252 - 줄 세우기

방탄 안티 아닙니다

https://www.acmicpc.net/problem/2252

2252번: 줄 세우기

예제 출력 결과를 의식하지 말자. 위상 정렬만 잘 구현하면 된다. 나는 당장 예제 2번의 출력 결과도 3 4 1 2가 나왔지만 정답은 맞았다.

 

위상 정렬을 구현하는 방법에는 두 가지가 존재한다.

 

1. Kahn 알고리즘

1) 그래프 최상단에 위치한 정점을 찾는다. 여기서 최상단이란 in-degree가 0인 정점을 말한다.

2) 해당 정점을 출력(정렬 완료로 표시)하고, 해당 정점과 연결된 간선을 모두 제거한다.

3) 만약 최상단에 아직 정점이 존재한다면 1)부터 다시 시작한다.

 

2. DFS

1) 방문하지 않은 정점을 찾는다.

2) 해당 정점에 연결된 모든 정점에 DFS를 수행한다. 이미 방문한 정점이라면 복귀한다.

3) DFS를 모두 마쳤으면 현재 정점을 방문 표시하고 맨 앞 부분에 출력한다.

4) 아직 방문하지 않은 정점이 있다면 1)부터 다시 시작한다.

 

2번 방식은 재귀적으로 작동한다. 또한 매 출력은 맨 앞에서 이루어지므로, deque를 사용하거나 원래의 출력 결과를 뒤집는 등의 처리가 필요하다.

 

두 방식의 수행 과정을 간단한 예시로 살펴보고, 이를 코드로 구현해보자. 동일 위상에서 출력 순서는 상관이 없으나 여기서는 노드 번호를 기준으로 순서를 정했다.

예시 그래프

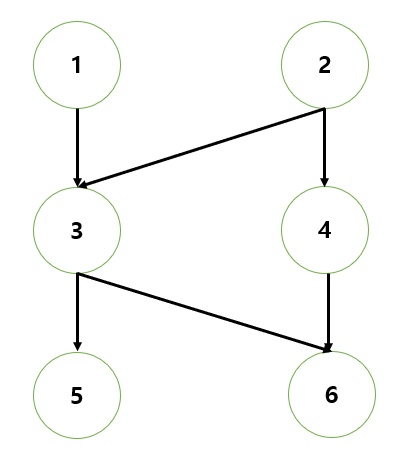
1. Kahn : 최상단 정점을 찾고, 출력한 뒤 연결된 간선을 삭제하는 과정을 반복

 

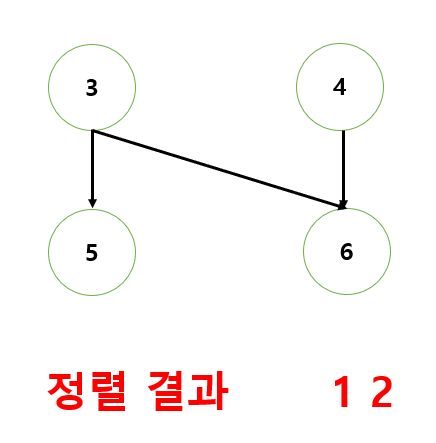
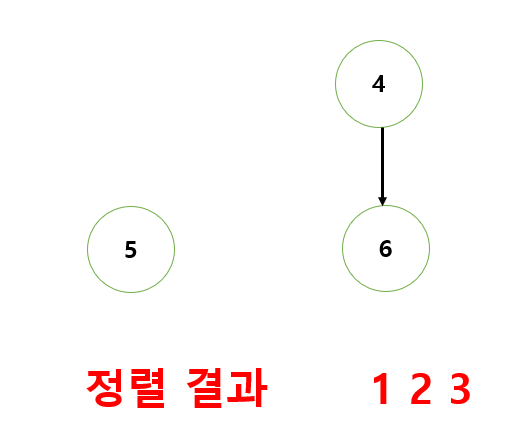
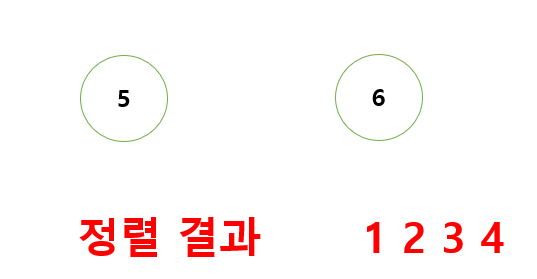
코드 구현

//유향 그래프이므로 in, out 간선을 각각 저장
vector<int> from[32001], to[32001];

void solve() {

	//Q : 최상단 정점을 저장하는 컨테이너
	queue<int> Q;

	for (int i = 1; i <= N; i++)
    	//최상단 정점 (in-degree가 0)인 경우
		if (from[i].empty())
			Q.push(i);

	int cur;
	while (!Q.empty()) {
    
    	//최상단 정점 중 하나를 선택해 출력
		cur = Q.front(); Q.pop();
		cout << cur << ' ';
		
        //연결된 간선을 삭제
		for (int nxt : to[cur]) {
			from[nxt].erase(find(from[nxt].begin(), from[nxt].end(), cur));
			
            //연결된 정점이 최상단에 위치하게 되면 큐에 추가
			if (from[nxt].empty())
				Q.push(nxt);
		}
	}

	cout << endl;
}

나는 실제 간선을 제거한다는 의미로 erase를 사용했는데, 굳이 그럴 것 없이 in-degree를 직접 저장하는 배열을 사용해 이런 식으로 구현해도 된다.

for (int nxt : to[cur]) {
	//간선 자체를 삭제하는 대신 in-degree 값만 감소
	in[nxt]--;
    
    //empty 대신 in[nxt] == 0을 사용
    if (!in[nxt])
        Q.push(nxt);
}

 

2. DFS 수행 후 결과 반전

현재 노드 : 3

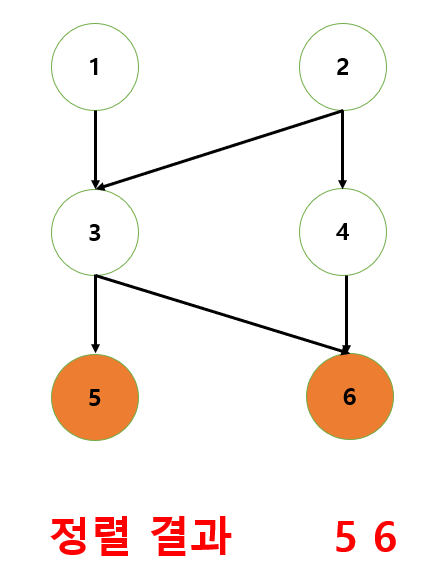
1번, 3번 노드는 아직 연결된 하위 정점에 대한 DFS가 끝나지 않았으므로 방문표시(주황색) 되지 않았다.

현재 노드 : 1

 

현재 노드 : 2

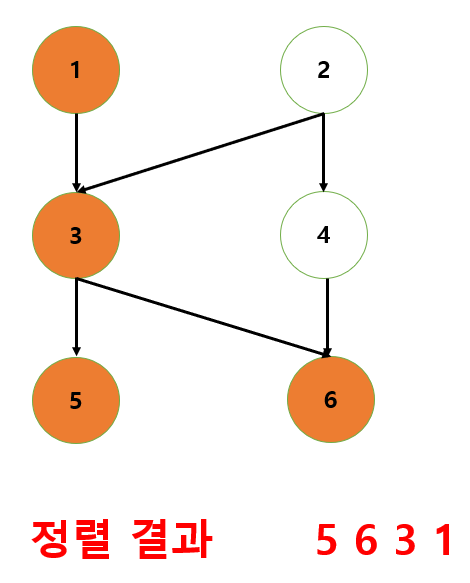
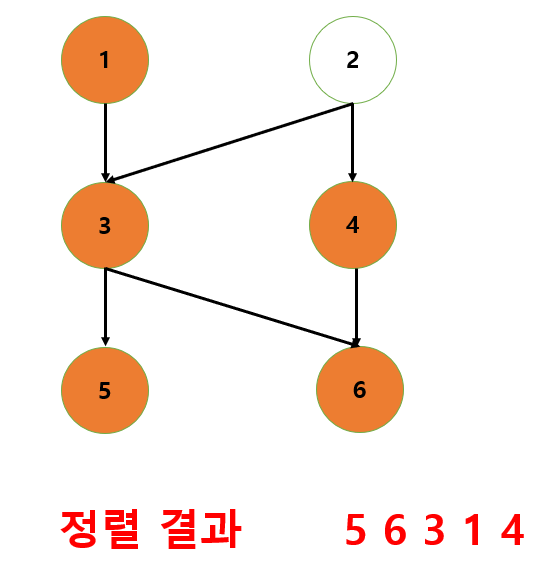
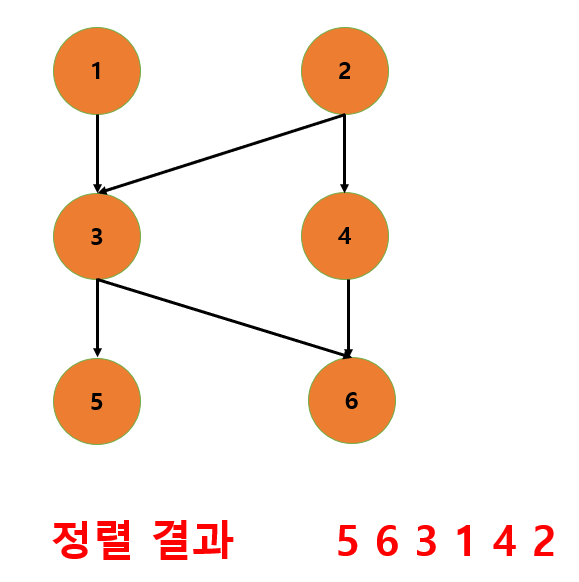
전체 DFS를 끝냈으면 결과를 반전한다.

 

코드는 재귀함수를 통한 DFS로 구현하면 된다. 실제 코드는 생략

 

 

두 방식이 정렬 결과는 다르지만, 둘 다 유효한 위상 정렬 방식이다. 위상 정렬은 존재하는 간선에 대해서만 정렬이 지켜지면 되기 때문이다. 즉 1이 3보다 앞에, 2가 3보다 앞에, 2가 4보다, 3이 5보다, 3이 6보다, 4가 6보다만 앞에 있으면 다른 순서는 어떻게 되든 상관없다. 이것이 위상 정렬의 핵심이다.