백준 3015 - 오아시스 재결합

두번째로 푼 플레티넘 문제 ㅎㅎ

https://www.acmicpc.net/problem/3015

3015번: 오아시스 재결합

 

0.

기본적인 문제 흐름은 스택을 활용해 크기를 비교하는 '오큰수' 류의 문제와 동일하다. 

 

스택에 '아직 나보다 큰 원소를 찾지 못한 원소의 크기'를 저장하고, 매번 새 원소를 추가하면서 새 원소보다 작은 원소들을 스택에서 제거하면 된다. 새 원소는 현재까지 확인한 원소 중 맨 끝에 있으므로 '나보다 큰 원소'가 존재하지 않아 무조건 스택에 추가된다.

1.

이제 쌍의 개수를 구할 차례이다. 구하는 방법은 단순하다. 스택에서 제거할 때마다 개수 카운터를 1씩 증가시키면 된다. 가능한 쌍 (A, B)는 다음의 3가지가 존재한다.

1번과 2번 쌍의 개수는 진행 방향이 서로 반대인 2개의 반복문으로 계산할 수 있다. 남들은 반복문 하나로 하던데;; 나는 무식하게 반복문을 두 개 썼다.

 

아래 코드는 2번 경우에 대한 반복문. 스택에서 원소를 제거할 때마다 카운터를 증가시키면 된다. 구간 설정만 거꾸로 하면 1번 경우를 계산할 수 있다.

for (int i = 0; i < N; i++) {
    while (!S.empty() && v[i] > S.top()) {
        sum++;
        S.pop();
    }
    S.push(v[i]);
}

2.

이 문제가 골드 수준의 스택 문제와 다른 점은 3번 경우가 추가됐다는 점이다. 위의 코드를 사용하면 크기가 같은 원소의 쌍은 확인할 수 없다. v[i] >= S.top() 처럼 부등호 조건만 바꾸면 되지 않을까? 아쉽게도 그렇게 날로 먹는 문제는 아니다.

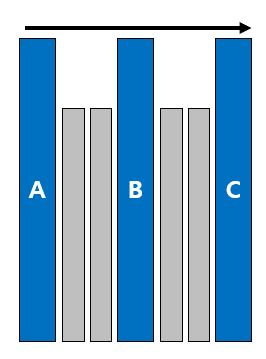
위 그림에서 가능한 3번 경우의 쌍은 (A,B), (B,C), (C,A) 3개이다. (회색 막대는 모두 크기가 다르다고 가정)

 

앞의 로직은 이렇게 동일한 크기의 쌍이 여러 개 존재할 때 문제가 생긴다. 원소 B를 추가했을 때, B >= A이기 때문에 카운터가 1 증가하며 (A, B) 쌍을 계산한다. 그러나 pop에 의해 A는 스택에서 제거되고, 따라서 C를 추가했을 때 (C, A) 쌍을 확인할 수 없게 된다.

 

결국 3번 경우의 핵심은 '새 원소와 크기가 같은 원소가 스택에서 사라지지 않게 하기' 라고 할 수 있겠다.

 

3.

동일 크기의 원소를 어떻게 유지할 수 있을까? 이것도 간단하다. while문 내부에서 동일 크기의 원소를 만날 경우, pop은 하되 만난 횟수를 기록한다. 그리고 while문이 끝나면 기록한 만큼 다시 스택에 push해주면 된다.

for (int i = 0; i < N; i++) {

    int cnt = 1; //새 원소 자신도 '동일 크기 원소'에 포함 → cnt 기본값 1
    
    while (!S.empty() && v[i] >= S.top()) {
        sum++;
    	if(v[i] == S.top())
        	cnt++;
        S.pop();
    }
    
    //동일 크기 원소 만난 만큼 다시 추가
    while(cnt) {
    	cnt--;
    	S.push(v[i]);
    }
}

앞에서 생성한 두 반복문 중 하나를 이런 식으로 수정하면, 간단한 TC는 모두 통과할 수 있을 것이다. 하지만 제출해보면 시간 초과가 걸린다. 문제는 새로 추가한 while문이다.

 

예를 들어 1번 원소부터 N번 원소까지 크기가 같다고 해보자.

>> 1번 원소를 추가할 때, 스택이 비어있으므로 스택에 원소가 1개 추가된다.

>> 2번 원소를 추가할 때, 원래 있던 원소 1개에 새 원소까지 스택에 원소가 총 2개 추가된다.

>> 3번 원소를 추가할 때, 원래 있던 원소 2개에 새 원소까지 스택에 원소가 총 3개 추가된다.

...

>> N번 원소를 추가할 때, 원래 있던 원소 N-1개에 새 원소까지 스택에 원소가 총 N개 추가된다.

 

이는 시간복잡도 O(N^2)의 연산이므로 50만 개의 원소가 모두 동일 크기라고 하면 시간 초과에 걸릴 수밖에 없다.

 

'만난 만큼 스택에 다시 추가한다'를 while문 없이 구현하는 방법이 있다. 스택 구조를 변경하면 된다.

stack<pair<int, int>>를 사용해, 스택에 '원소 번호'와 함께 '스택에 있던 동일 크기 원소의 개수'를 저장한다고 하자. 

 

이제 스택에 크기 5인 원소 4개를 일일히 저장할 필요 없이 {5, 4}만 추가하면 된다.

 

그럼 바로 위 프로그램의 구문을 다음과 같이 변경할 수 있다.

 

>> sum++ → sum += S.top().second

S의 top에 있는 원소가 {a, b}라고 하자. 스택에 정의에 따르면, 아직 자신보다 큰 원소를 찾지 못한 크기 a의 원소가 현재 b개 존재한다. 만약 v[i]가 a보다 크거나 같다고 하면 이 b개의 원소들은 모두 원소 i와 쌍을 이룰 수 있으므로, 가능한 쌍의 개수가 b개 추가된다.

 

>> cnt++ → cnt = S.top().second + 1

만약 새 원소의 크기가 a와 같을 경우, 아직 자신보다 큰 원소를 찾지 못한 크기 a의 원소 개수는 새 원소까지 포함하여 b + 1개가 된다.

 

>> while(cnt)... → S.push({v[i], cnt})

시간초과를 해결하는 핵심이다. while문이 끝나고 나면 새 원소를 스택에 추가한다. 이 때 cnt가 갖는 값은 스택에 v[i]와 동일 크기의 원소가 없었다면 초기값인 1, v[i] = a인 원소 {a, b}가 있었다면 b+1이 된다. 따라서 새 원소와 동일 크기의 원소들의 정보를 O(1)의 연산으로 스택에서 보존할 수 있다.

 

마지막으로 50만 명의 사람이 만들 수 있는 쌍의 최대 개수를 고려하며 답을 출력하면 된다. (sum 자료형 long long으로 하라는 뜻)